I wrote a (very long) blog post about those viral math problems and am looking for feedback, especially from people who are not convinced that the problem is ambiguous.
It’s about a 30min read so thank you in advance if you really take the time to read it, but I think it’s worth it if you joined such discussions in the past, but I’m probably biased because I wrote it :)
Honestly, I do disagree that the question is ambiguous. The lack of parenthetical separation is itself a choice that informs order of operations. If the answer was meant to be 9, then the 6/2 would be isolated in parenthesis.
It’s covered in the blog, but this is likely due to a bias towards Strong Juxtaposition rules for parentheses rather than Weak. It’s common for those who learned math into advanced algebra/ beginning Calc and beyond, since that’s the usual method for higher math education. But it isn’t “correct”, it’s one of two standard ways of doing it. The ambiguity in the question is intentional and pervasive.
My argument is specifically that using no separation shows intent for which way to interpret and should not default to weak juxtaposition.
Choosing not to use (6/2)(1+2) implies to me to use the only other interpretation.
There’s also the difference between 6/2(1+2) and 6/2*(1+2). I think the post has a point for the latter, but not the former.
I don’t know what you want, man. The blog’s goal is to describe the problem and why it comes about and your response is “Following my logic, there is no confusion!” when there clearly is confusion in the wider world here. The blog does a good job of narrowing down why there’s confusion, you’re response doesn’t add anything or refute anything. It’s just… you bragging? I’m not certain what your point is.
your response is “Following my logic, there is no confusion!”
That’s because the actual rules of Maths have all been followed, including The Distributive Law and Terms.
there clearly is confusion in the wider world here
Amongst people who don’t remember The Distributive Law and Terms.
The blog does a good job of narrowing down why there’s confusion
The blog ignores The Distributive Law and Terms. Notice the complete lack of Maths textbook references in it?
I originally had the same reasoning but came to the opposite conclusion. Multiplication and division have the same precedence, so I read the operations from left to right unless noted otherwise with parentheses. Thus:
6/2=3
3(1+2)=9
For me to read the whole of 2(1+2) as the denominator in a fraction I would expect it to be isolated in parentheses: 6/(2(1+2)).
Reading the blog post, I understand the ambiguity now, but i’m still fascinated that we had the same criticism (no parentheses implies intent) but had opposite conclusions.
6/2=3
3(1+2)=9
You just did division before brackets, which goes against order of operations rules.
For me to read the whole of 2(1+2) as the denominator in a fraction
You just need to know The Distributive Law and Terms.
Read the linked article
The linked article is wrong. Read this - has, you know, actual Maths textbook references in it, unlike the article.
But it isn’t “correct”
It is correct - it’s The Distributive Law.
it’s one of two standard ways of doing it.
There’s only 1 way - the “other way” was made up by people who don’t remember The Distributive Law and/or Terms (more likely both), and very much goes against the standards.
The ambiguity in the question is
…zero.
Hooray! Correct! Anyone who downvoted or disagrees with this needs to read this instead. Includes actual Maths textbooks references.
Did you read the blog post?
deleted by creator
The blog post is fine
Except that it’s wrong. Read this instead.
Nope it’s bedmas since everything is brackets
Seems this whole thing is the pedestrian-math-nerd’s equivalent to the pedestrian-grammar-nerd’s arguments on the Oxford comma. At the end of the day it seems mathematical notation is just as flexible as any other facet of written human communication and the real answer is “make things as clear as possible and if there is ambiguity, further clarify what you are trying to communicate.”
Pretty much. While it’s worth knowing that not everyone agrees on how implicit multiplication is prioritised, anywhere that everyone agreeing on the answer actually mattered, you wouldn’t write an equation as ambiguous as this one in the first place
It’s not ambiguous. People who say it is have usually forgotten The Distributive Law or Terms, or more commonly both!
Seems this whole thing is the pedestrian-math-nerd’s equivalent to the pedestrian-grammar-nerd’s arguments on the Oxford comma.
Not even remotely similar. Maths rules are fixed. The order of operations rules are at least 400 years old.
mathematical notation is just as flexible as any other facet of written human communication
No, it isn’t. The book “A history of mathematical notation” is in itself more than 100 years old.
Wow neat, and yet the thread was full of people going back and forth about how the equation can be misinterpreted based on how the order of operations can be interpreted. Thanks for your months later input though.
I only just found the thread yesterday. There’s only 1 “interpretation”, and the only back and forth I’ve seen about interpretations is about implicit multiplication, which isn’t a thing, at all - it’s people conflating The Distributive Law and Terms dotnet.social/@SmartmanApps/110925761375035558
So you are saying exactly what I said; people can misinterpret things that other people have written. Good job. Thanks again for stopping by a 3 month old thread about a dumb meme.
So you are saying exactly what I said; people can misinterpret things that other people have written
No, I’m not. They’re “misinterpreting” something that isn’t even a rule of Maths. There’s no way to misinterpret the actual rules, there’s no way to misinterpret the equation. There’s no alternative interpretations of the notation. Someone who didn’t remember the rules literally made up “implicit multiplication”, and then other people argued with them about what that meant. 😂
You look like a real idiot here. I really suggest you actually read the article instead of “scanning” it. You clearly don’t even understand the term “implicit multiplication” if you’re claiming it’s made up. Implicit multiplication is not the controversial part of this equation, which you would know if you read the article and understood what people in this thread are even talking about. Stop spamming your shitty blog and just. Read. The. Article.
read the article instead of “scanning” it.
I stopped reading as soon as I saw the claim that the right answer was wrong. I then scanned it for any textbook references, and there were none (as expected).
You clearly don’t even understand the term “implicit multiplication” if you’re claiming it’s made up
Funny that you use the word “term”, since Terms are ONE of the things that people are referring to when they say “implicit multiplication” - the other being The Distributive Law. i.e. Two DIFFERENT actual rules of Maths have been lumped in together in a made-up rule (by people who don’t remember the actual rules).
BTW if you think it’s not made-up then provide me with a Maths textbook reference that uses it. Spoiler alert: you won’t find any.
Implicit multiplication is not the controversial part of this equation
It’s not the ONLY controversial part of the equation - people make other mistakes with it too - but it’s the biggest part. It’s the mistake that most people have made.
shitty blog
So that’s what you think of people who educate with actual Maths textbook references?
Read. The. Article.
Read Maths textbooks.
@wischi “Funny enough all the examples that N.J. Lennes list in his letter use implicit multiplications and thus his rule could be replaced by the strong juxtaposition”.
Weird they didn’t need two made-up terms to get it right 100 years ago.
Indeed Duncan. :-)
his rule could be replaced by the strong juxtaposition
“strong juxtaposition” already existed even then in Terms (which Lennes called Terms/Products, but somehow missed the implication of that) and The Distributive Law, so his rule was never adopted because it was never needed - it was just Lennes #LoudlyNotUnderstandingThings (like Terms, which by his own admission was in all the textbooks). 1917 (ii) - Lennes’ letter (Terms and operators)
In other words…
Funny enough all the examples that N.J. Lennes list in his letter use
…Terms/Products., as we do today in modern high school Maths textbooks (but we just use Terms in this context, not Products).
Damn ragebait posts, it’s always the same recycled operation. They could at least spice it up, like the discussion about absolute value. What’s |a|b|c|?
What I gather from this, is that Geogebra is superior for not allowing ambiguous notation to be parsed 👌
Your example with the absolute values is actually linked in the “Even more ambiguous math notations” section.
Geogebra has indeed found a good solution but it only works if you input field supports fractions and a lot of calculators (even CAS like WolframAlpha) don’t support that.
Even more ambiguous math notations
Except that isn’t ambiguous either. See my reply to the original comment.
Geogebra has indeed found a good solution
Geogebra has done the same thing as Desmos, which is wrong. Desmos USED TO give correct answers, but then they changed it to automatically interpret / as a fraction, which is good, except when they did that it ALSO now interprets ÷ as a fraction, which is wrong. ½ is 1 term, 1÷2 is 2 terms (but Desmos now treats it as 1 term, which goes against the definition of terms)
What’s |a|b|c|?
The absolute value of a, times b, times the absolute value of c (which would be more naturally written as b|ac|). Unlike brackets, there’s no such thing as nested absolute value. If you wanted it to read as the absolute value of (a times the absolute value of b times c), then that’s EXACTLY the same answer as the absolute value of (a times b times c), which is why nested absolute values make no sense - you only have to take absolute value once to get rid of all the contained signs.
I don’t remember everything, but I remember the first two operations are exponents then parentheses. Edit: wait is it the other way around?
Yes it’s the other way round. Parentheses are top priority.
The full story is actually more nuanced than most people think, but the post is actually very long (about 30min) so thank you in advance if you really find the time to read it.
bidmas
brackets, index (powers), division, multiplication, addition, subtraction.
brackets are always first that’s the whole point of brackets
You guys are doing it all wrong: ask chatgpt for the correct answer and paste it here. Done.
Who needs to learn or know anything really?
ChatGPT says…

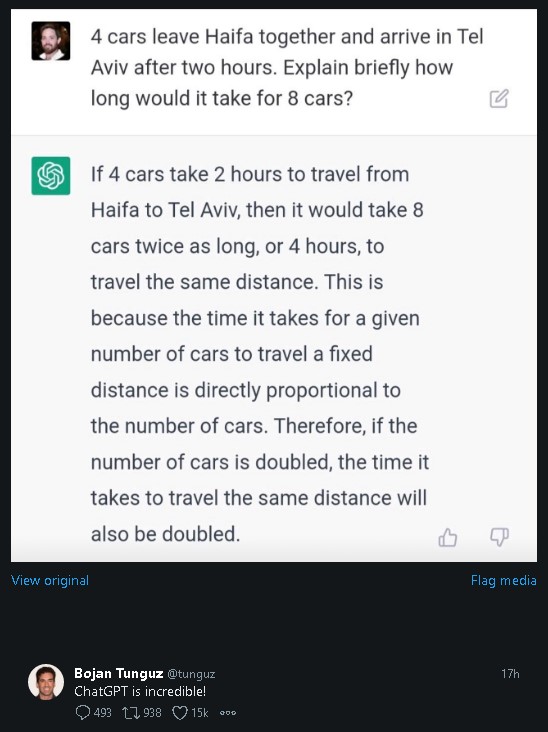
ChatGPT’s Answer:
The expression 6/2(1+2) involves both multiplication and division. According to the order of operations (PEMDAS/BODMAS), you should perform operations inside parentheses first, then any multiplication or division from left to right.
Let’s break down the expression step by step:
Inside the parentheses: 1 + 2 = 3
Now the expression becomes 6/2 * 3
Division: 6/2 = 3
Multiplication: 3 * 3 = 9
So, 6/2(1+2) is equal to 9.
Ackshually, the answer is 4
6÷2*(1+2)
6÷(1+2)*2
6÷(3)*2
2*2
4
You’re welcome
If there are rules about which dot comes first then you are not allowed to do this.
You aren’t allowed to do this because division isn’t transitive.
In fact you’re not allowed to add the multiplication - it breaks up the factorised term, hence gives a different answer.
The rule is you’re not allowed to add dots (multiplication) - broke up the factorised term, which is why a different answer.
psychopath
The ambiguous ones at least have some discussion around it. The ones I’ve seen thenxouple times I had the misfortune of seeing them on Facebook were just straight up basic order of operations questions. They weren’t ambiguous, they were about a 4th grade math level, and all thenpeople from my high-school that complain that school never taught them anything were completely failing to get it.
I’m talking like 4+1x2 and a bunch of people were saying it was 10.
Great read! Easy for everyone to understand, but also thorough. I loved the breakdown into the calculators functionality
Not thorough at all. Never once referenced an actual Maths textbook. Read this instead.
I disagree. Without explicit direction on OOO we have to follow the operators in order.
The parentheses go first. 1+2=3
Then we have 6 ÷2 ×3
Without parentheses around (2×3) we can’t do that first. So OOO would be left to right. 9.
In other words, as an engineer with half a PhD, I don’t buy strong juxtaposition. That sounds more like laziness than math.
as an engineer with half a PhD
As an engineer with a full PhD. I’d say we engineers aren’t that great with math problems like this. Thus any responsible engineer would write it in a way that cannot be misinterpreted. Because misinterpreted mathematics can kill people…
As an engineer with a full PhD. I’d say we engineers aren’t that great with math problems like this
Yay for a voice of reason! I’ve yet to see anyone who says they have a Ph.D. get this correct (I’m a high school Maths teacher/tutor - I actually teach this topic).
as a half PhD
Go read the article, it’s about you
Go read the article, it’s about you
The article is wrong dotnet.social/@SmartmanApps/110897908266416158
Yeah, but implicit multiplication without a sign is often treated with higher priority.
Is it though? I’ve only ever seen it treated as standard multiplication.
Read TFA
Sure. That doesn’t mean it’s right to do.
Please read the article, that’s exactly what it’s about. There is no right answer.
There is a right answer. Read this instead dotnet.social/@SmartmanApps/110897908266416158
I read the article, and it explained the situation and the resultant confusion very well. That said, could we not have some international body just make a decision one way or the other, instead of perpetuating this uncertainty?
could we not have some international body just make a decision one way or the other
There’s no decision to be made. The correct rules are already taught in literally every Year 7-8 Maths textbook.
Without parentheses around (2×3)
But there is parentheses around (2x3). a(b+c)=(ab+ac) - The Distributive Law. You can’t remove them unless there is only 1 term left inside. You removed them when you still had 2 terms inside, 2x3.
6/2(1+2)=6/2(3)=6/(2*3)=6/6=1
OR
6/2(1+2)=6/(2+4)=6/6=1
How are people upvoting you for refusing to read the article?
I did read the article. I am commenting that I have never encountered strong juxtaposition and sharing why I think it is a poor choice.
You probably missed the part where the article talks about university level math, and that strong juxtaposition is common there.
I also think that many conventions are bad, but once they exist, their badness doesn’t make them stop being used and relied on by a lot of people.
I don’t have any skin in the game as I never ran into ambiguity. My university professors simply always used fractions, therefore completely getting rid of any possible ambiguity.
You probably missed the part where the article talks about university level math,
This is high school level Maths. It’s not taught at university.
I have never encountered strong juxtaposition
There’s “strong juxtaposition” in both Terms and The Distributive Law - you’ve never encountered either of those?
Because as a high school Maths teacher as soon as I saw the assertion that it was ambiguous I knew the article was wrong. From there I scanned to see if there were any Maths textbooks at any point, and there wasn’t. Just another wrong article.
Lol. Read it.
Why would I read something that I know is wrong? #MathsIsNeverAmbiguous
Mathematical notation however can be. Because it’s conventions as long as it’s not defined on the same page.
Mathematical notation however can be.
Nope. Different regions use different symbols, but within those regions everyone knows what each symbol is, and none of those symbols are in this question anyway.
Because it’s conventions as long as it’s not defined on the same page
The rules can be found in any high school Maths textbook.
Let’s do a little plausibility analysis, shall we? First, we have humans, you know, famously unable to agree on an universal standard for anything. Then we have me, who has written a PhD thesis for which he has read quite some papers about math and computational biology. Then we have an article that talks about the topic at hand, but that you for some unscientific and completely ridiculous reason refuse to read.
Let me just tell you one last time: you’re wrong, you should know that it’s possible that you’re wrong, and not reading a thing because it could convince you is peak ignorance.
I’m done here, have a good one, and try not to ruin your students too hard.
Because those people also didn’t read the article and are reacting from their gut.
are reacting from their gut
As was the person who wrote the article. Did you not notice the complete lack of Maths textbooks in it?
Starting a new comment thread (I gave up on reading all of them). I’m a high school Maths teacher/tutor. You can read my Mastodon thread about it at Order of operations thread index (I’m giving you the link to the thread index so you can just jump around whichever parts you want to read without having to read the whole thing). Includes Maths textbooks, historical references, proofs, memes, the works.
And for all the people quoting university people, this topic (order of operations) is not taught at university - it is taught in high school. Why would you listen to someone who doesn’t teach the topic? (have you not wondered why they never quote Maths textbooks?)
#DontForgetDistribution #MathsIsNeverAmbiguous
I’m curious if you actually read the whole (admittedly long) page linked in this post, or did you stop after realizing that it was saying something you found disagreeable?
I’m a high school Maths teacher/tutor
What will you tell your students if they show you two different models of calculator, from the same company, where the same sequence of buttons on each produces a different result than on the other, and the user manuals for each explain clearly why they’re doing what they are? “One of these calculators is just objectively wrong, trust me on this, #MathsIsNeverAmbiguous” ?
The truth is that there are many different math notations which often do lead to ambiguities.
In the case of the notation you’re dismissing in your (hilarious!) meme here, well, outside of anglophone high schools, people don’t often encounter the obelus notation for division at all except for as a button on calculators. And there its meaning is ambiguous (as clearly explained in OP’s link).
Check out some of the other things which the “÷” symbol can mean in math!
#MathNotationsAreOftenAmbiguous
did you stop after realizing that it was saying something you found disagreeable
I stopped when he said it was ambiguous (it’s not, as per the rules of Maths), then scanned the rest to see if there were any Maths textbook references, and there wasn’t (as expected). Just another wrong blog.
What will you tell your students if they show you two different models of calculator, from the same company
Has literally never happened. Texas Instruments is the only brand who continues to do it wrong (and it’s right there in their manual why) - all the other brands who were doing it wrong have reverted back to doing it correctly (there’s a Youtube video about this somewhere). I have a Sharp calculator (who have literally always done it correctly) and most of my students have Casio, so it’s never been an issue.
trust me on this
I don’t ask them to trust me - I’m a Maths teacher, I teach them the rules of Maths. From there they can see for themselves which calculators are wrong and why. Our job as teachers is for our students to eventually not need us anymore and work things out for themselves.
The truth is that there are many different math notations which often do lead to ambiguities
Not within any region there isn’t. e.g. European countries who use a comma instead of a decimal point. If you’re in one of those countries it’s a comma, if you’re not then it’s a decimal point.
people don’t often encounter the obelus notation for division at all
In Australia it’s the only thing we ever use, and from what I’ve seen also the U.K. (every U.K. textbook I’ve seen uses it).
Check out some of the other things which the “÷” symbol can mean in math!
Go back and read it again and you’ll see all of those examples are worded in the past tense, except for ISO, and all ISO has said is “don’t use it”, for reasons which haven’t been specified, and in any case everyone in a Maths-related position is clearly ignoring them anyway (as you would. I’ve seen them over-reach in Computer Science as well, where they also get ignored by people in the industry).
Has literally never happened. Texas Instruments is the only brand who continues to do it wrong […] all the other brands who were doing it wrong have reverted
Ok so you’re saying it never happened, but then in the very next sentence you acknowledge that you know it is happening with TI today, and then also admit you know that it did happen with some other brands in the past?
But, if you had read the linked post before writing numerous comments about it, you’d see that it documents that the ambiguity actually exists among both old and currently shipping models from TI, HP, Casio, and Canon, today, and that both behaviors are intentional and documented.
There is no bug; none of these calculators is “wrong”.
The truth is that there are many different math notations which often do lead to ambiguities
Not within any region there isn’t.
Ok, this is the funniest thing I’ve read so far today, but if this is what you are teaching high school students it is also rather sad because you are doing them a disservice by teaching them that there is no ambiguity where there actually is.
If OP’s blog post is too long for you (it is quite long) i recommend reading this one instead: The PEMDAS Paradox.
In Australia it’s the only thing we ever use, and from what I’ve seen also the U.K. (every U.K. textbook I’ve seen uses it).
By “we” do you mean high school teachers, or Australian society beyond high school? Because, I’m pretty sure the latter isn’t true, and I’m skeptical of the former. I thought generally the ÷ symbol mostly stops being used (except as a calculator button) even before high school, basically as soon as fractions are taught. Do you have textbooks where the fraction bar is used concurrently with the obelus (÷) division symbol?
Ok so you’re saying it never happened, but then in the very next sentence you acknowledge that you know it is happening with TI today
You asked me what I do if my students show me 2 different answers what do I tell them, and I told you that has never happened. None of my students have ever had one of the calculators which does it wrong.
that both behaviors are intentional and documented
Correct. I already noted earlier (maybe with someone else) that the TI calculator manual says that they obey the Primary School order of operations, which doesn’t work with High School order of operations. i.e. when the brackets have a coefficient. The TI calculator will give a correct answer for 6/(1+2) and 6/2x(1+2), but gives a wrong answer for 6/2(1+2), and it’s in their manual why. I saw one Youtuber who was showing the manual scroll right past it! It was right there on screen why it does it wrong and she just scrolled down from there without even looking at it!
none of these calculators is “wrong”.
Any calculator which fails to obey The Distributive Law is wrong. It is disobeying a rule of Maths.
there is no ambiguity where there actually is.
There actually isn’t. We use decimal points (not commas like some European countries), the obelus (not colon like some European countries), etc., so no, there is never any ambiguity. And the expression in question here follows those same notations (it has an obelus, not a colon), so still no ambiguity.
i recommend reading this one instead: The PEMDAS Paradox
Yes, I’ve read that one before. Makes the exact same mistakes. Claims it’s ambiguous while at the same time completely ignoring The Distributive Law and Terms. I’ll even point out a specific thing (of many) where they miss the point…
So the disagreement distills down to this: Does it feel like a(b) should always be interchangeable with axb? Or does it feel like a(b) should always be interchangeable with (ab)? You can’t say both.
ab=(axb) by definition. It’s in Cajori, it’s in today’s Maths textbooks. So a(b) isn’t interchangeable with axb, it’s only interchangeable with (axb) (or (ab) or ab). That’s one of the most common mistakes I see. You can’t remove brackets if there’s still more than 1 term left inside, but many people do and end up with a wrong answer.
By “we” do you mean high school teachers, or Australian society beyond high school?
I said “In Australia” (not in Australian high school), so I mean all of Australia.
Because, I’m pretty sure the latter isn’t true
Definitely is. I have never seen anyone here ever use a colon to mean divide. It’s only ever used for a ratio.
Do you have textbooks where the fraction bar is used concurrently with the obelus (÷) division symbol?
All my textbooks use both. Did you read my thread? If you use a fraction bar then that is a single term. If you use an obelus (or colon if you’re in a country which uses colon for division) then that is 2 terms. I covered all of that in my thread.
EDITED TO ADD: If you don’t use both then how do you write to divide by a fraction?
Here is an alternative Piped link(s):
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I’m open-source; check me out at GitHub.
That’s cool and Imma let you finish but I’m not a mathematician and the answer is 9.
I’m not a mathematician and the answer is 9
I’m a Mathematician and the answer is 1.
That’s the correct answer if you follow one of the conventions. There are actually two conflicting but equally valid conventions. The blog explains the full story but this math problem is really ambiguous.
I read it. And I’m not a mathematician, so the answer is 9.
E: The salty mathematicians down-voting this can get fucked lmfao
That’s the correct answer if you follow
…the rules of Maths.
isn’t that division sign I only saw Americans use written like this (÷) means it’s a fraction? so it’s 6÷2, since the divisor (or what is it called in english, the bottom half of the fraction) isn’t in parenthesis, so it would be foolish to put the whole 2(1+2) down there, there’s no reason for that.
so it’s (6/2)*(1+2) which is 3*3 = 9.
the other way around would be 6÷(2(1+2)) if the whole expression is in the divisor and than that’s 1.
tho I’m not really proficient in math, I have eventually failed it in university, but if I remember my teachers correctly, this should be the way. but again, where I live, we never use the ÷ sign, only in elementary school where we divide on paper. instead we use the fraction form, and with that, these kind of seemingly ambiguous expressions doesn’t exist.
It seems Americans are taught pemdas and not bodas.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
So Americans will multiply anything first. This is why I put 6 ÷ ( n*(n – 1)) in excel to avoid confusion.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
Yeah, there’s a problem with some lazy textbook authors, which I talked about here. A term is defined as ab=(axb), and yet many textbooks lazily write it as ab=axb, which is fine if that’s the whole expression, but NOT fine if the expression is a/bc (a/(bxc) and a/bxc AREN’T the same thing!), and so we end up with people removing brackets prematurely and getting wrong answers. In other words, in your case, only n!=n(n – 1) and n!=(nx(n – 1)) can be used interchangeably.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
yeah, the way I have been taught is that either you put the multiplication sign there or not, it’s the exact same, there’s absolutely no difference in n(n-1) and n*(n-1). in the end, you treat it like the * sign is there and it’s just matter of convenience you can leave it off.
there’s absolutely no difference in n(n-1) and n*(n-1)
There is - the first is 1 term and the 2nd is 2 terms. Makes a difference if it’s preceded by a division.
it’s just matter of convenience you can leave it off.
It’s a matter of how many terms as to whether it’s there or not.
deleted by creator
The ÷ sign isn’t used by “Americans”, it’s used by small children. As soon as you learn basic mathematical notation in your introductory algebra class, you’ve outgrown the use of that symbol.
The ÷ sign isn’t used by “Americans”, it’s used by small children
I don’t know where you’re from, but it’s used universally in Australia - textbooks, calculators, all ages - and from what I’ve seen the U.K. too.
Children here in the Netherlands use : as a divisor symbol. I don’t know whether the ÷ sign is particularly American, but it’s not universal.
written like this (÷) means it’s a fraction?
No, that means it’s a division. i.e. a÷b. To indicate it’s a fraction it would need to be written as (a÷b). i.e. make it a single term. Terms are separated by operators and joined by grouping symbols (such as brackets or fraction bars).
put the whole 2(1+2) down there, there’s no reason for that.
There is - it’s a single bracketed term, subject to The Distributive Law. i.e. the B in BEDMAS.